
R. Sinatra, P. Deville, M. Szell, D. Wang, A.-L. Barabási
A century of physics
Nature Physics 11, 791-796 (2015)
Read the abstract
An analysis of Web of Science data spanning more than 100 years reveals the rapid growth andincreasing multidisciplinary of physics — as well its internal map of sub-disciplines.
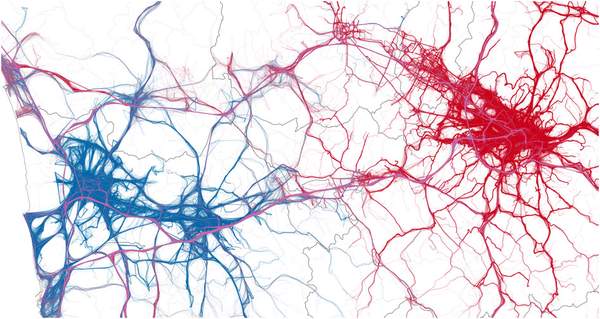
L. Pappalardo, F. Simini, S. Rinzivillo, D. Pedreschi, F. Giannotti, A.-L. Barabási
Returners and explorers dichotomy in human mobility
Nature Communications 6:8166, 1-8 (2015)
Read the abstract
The availability of massive digital traces of human whereabouts has offered a series of novel insights on the quantitative patterns characterizing human mobility. In particular, numerous recent studies have lead to an unexpected consensus: the considerable variability in the characteristic travelled distance of individuals coexists with a high degree of predictability of their future locations. Here we shed light on this surprising coexistence by systematically investigating the impact of recurrent mobility on the characteristic distance travelled by individuals. Using both mobile phone and GPS data, we discover the existence of two distinct classes of individuals: returners and explorers. As existing models of human mobility cannot explain the existence of these two classes, we develop more realistic models able to capture the empirical findings. Finally, we show that returners and explorers play a distinct quantifiable role in spreading phenomena and that a correlation exists between their mobility patterns and social interactions.
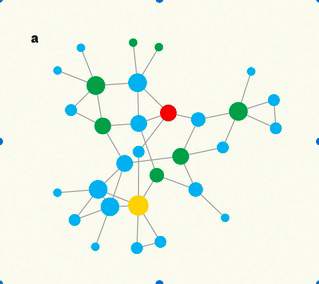
I. A. Kovács, A.-L. Barabási
Destruction perfected
Nature (News & Views) 524, 38-39 (2015)
Read the abstract
Pinpointing the nodes whose removal most effectively disrupts a network has become a lot easier with the development of an efficient algorithm. Potential applications might include cybersecurity and disease control. See Letter p.65, by F. Morone and H. A. Makse (Supplementary 1).
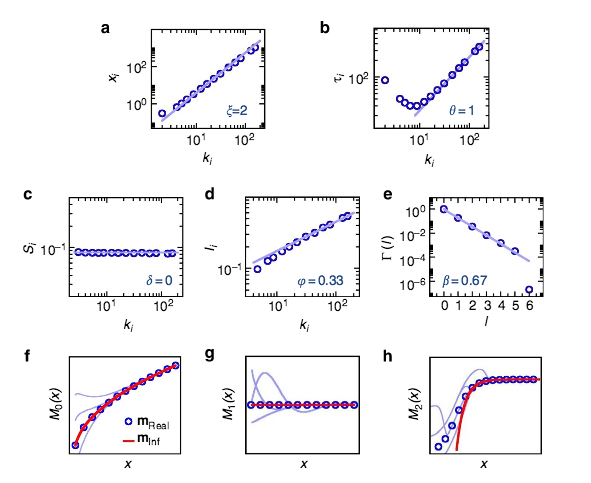
B. Barzel, Y.-Y. Liu, A.-L. Barabási
Constructing minimal models for complex system dynamics
Nature Communications 6:7186, 1-8 (2015)
Read the abstract
One of the strengths of statistical physics is the ability to reduce macroscopic observations into microscopic models, offering a mechanistic description of a system’s dynamics. This paradigm, rooted in Boltzmann’s gas theory, has found applications from magnetic phenomena to subcellular processes and epidemic spreading. Yet, each of these advances were the result of decades of meticulous model building and validation, which are impossible to replicate in most complex biological, social or technological systems that lack accurate microscopic models. Here we develop a method to infer the microscopic dynamics of a complex system from observations of its response to external perturbations, allowing us to construct the most general class of nonlinear pairwise dynamics that are guaranteed to recover the observed behavior. The result, which we test against both numerical and empirical data, is an effective dynamic model that can predict the system’s behavior and provide crucial insights into its inner workings.

J. Menche, A. Sharma, M. Kitsak, D. Ghiassian, M. Vidal, J. Loscazlo, A.-L. Barabasi
Uncovering disease-disease relationships through the incomplete interactome
Science 347:6224, 1257601-1 (2015)
Read the abstract
According to the disease module hypothesis, the cellular components associated with a disease segregate in the same neighborhood of the human interactome, the map of biologically relevant molecular interactions. Yet, given the incompleteness of the interactome and the limited knowledge of disease-associated genes, it is not obvious if the available data have sufficient coverage to map out modules associated with each disease. Here we derive mathematical conditions for the identifiability of disease modules and show that the network-based location of each disease module determines its pathobiological relationship to other diseases. For example, diseases with overlapping network modules show significant coexpression patterns, symptom similarity, and comorbidity, whereas diseases residing in separated network neighborhoods are phenotypically distinct. These tools represent an interactome-based platform to predict molecular commonalities between phenotypically related diseases, even if they do not share primary disease genes.
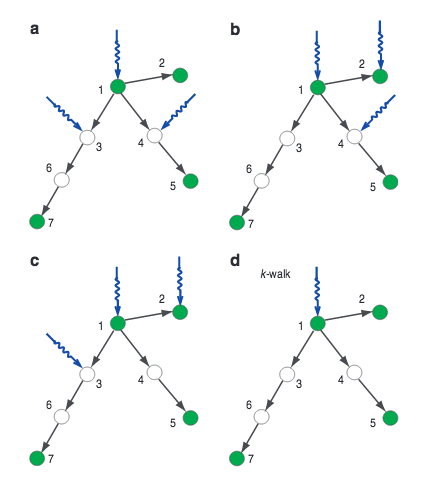
Jianxi Gao, Y.-Y.Liu, R. M. D'Souza, A.-L. Barabási
Target control of complex networks
Nature Communications 5:5415, 1-7 (2014)
Read the abstract
Controlling large natural and technological networks is an outstanding challenge. It is typically neither feasible nor necessary to control the entire network, prompting us to explore target control: the efficient control of a preselected subset of nodes. We show that the structural controllability approach used for full control overestimates the minimum number of driver nodes needed for target control. Here we develop an alternate ‘k-walk’ theory for directed tree networks, and we rigorously prove that one node can control a set of target nodes if the path length to each target node is unique. For more general cases, we develop a greedy algorithm to approximate the minimum set of driver nodes sufficient for target control. We find that degree heterogeneous networks are target controllable with higher efficiency than homogeneous networks and that the structure of many real-world networks are suitable for efficient target control.
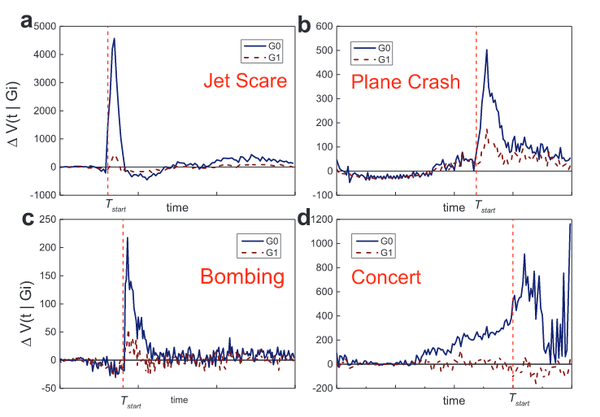
L. Gao, C. Song, Z. Gao, A.-L. Barabasi, J. P. Bagrow, D. Wang
Quantifying information flow during emergencies
Scientific Reports 4, 1-6 (2014)
Read the abstract
Recent advances on human dynamics have focused on the normal patterns of human activities, with the quantitative understanding of human behavior under extreme events remaining a crucial missing chapter. This has a wide array of potential applications, ranging from emergency response and detection to traffic control and management. Previous studies have shown that human communications are both temporally and spatially localized following the onset of emergencies, indicating that social propagation is a primary means to propagate situational awareness. We study real anomalous events using country-wide mobile phone data, finding that information flow during emergencies is dominated by repeated communications. We further demonstrate that the observed communication patterns cannot be explained by inherent reciprocity in social networks, and are universal across different demographics.
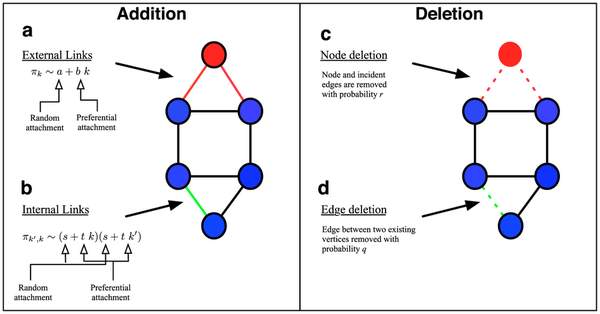
G. Ghoshal, L. Chi, A.-L. Barabási
Uncovering the role of elementary processes in network evolution
Scientifc Reports 3, 1-8 (2013)
Read the abstract
The growth and evolution of networks has elicited considerable interest from the scientific community and a number of mechanistic models have been proposed to explain their observed degree distributions. Various microscopic processes have been incorporated in these models, among them, node and edge addition, vertex fitness and the deletion of nodes and edges. The existing models, however, focus on specific combinations of these processes and parameterize them in a way that makes it difficult to elucidate the role of the individual elementary mechanisms. We therefore formulated and solved a model that incorporates the minimal processes governing network evolution. Some contribute to growth such as the formation of connections between existing pair of vertices, while others capture deletion; the removal of a node with its corresponding edges, or the removal of an edge between a pair of vertices. We distinguish between these elementary mechanisms, identifying their specific role on network evolution.
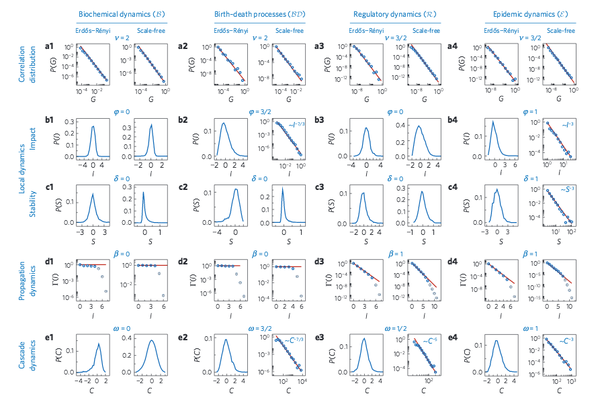
B. Barzel, A.-L. Barabási
Universality in network dynamics
Nature Physics 9, 673-681 (2013)
Read the abstract
Despite significant advances in characterizing the structural properties of complex networks, a mathematical framework that uncovers the universal properties of the interplay between the topology and the dynamics of complex systems continues to elude us. Here we develop a self-consistent theory of dynamical perturbations in complex systems, allowing us to systematically separate the contribution of the network topology and dynamics. The formalism covers a broad range of steady-state dynamical processes and offers testable predictions regarding the system’s response to perturbations and the development of correlations. It predicts several distinct universality classes whose characteristics can be derived directly from the continuum equation governing the system’s dynamics and which are validated on several canonical network-based dynamical systems, from biochemical dynamics to epidemic spreading. Finally, we collect experimental data pertaining to social and biological systems, demonstrating that we can accurately uncover their universality class even in the absence of an appropriate continuum theory that governs the system’s dynamics.
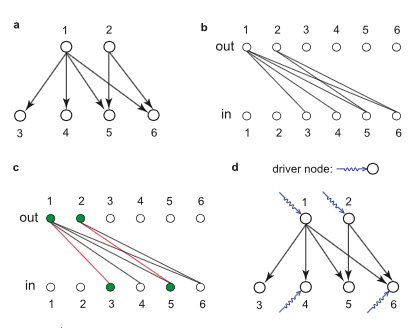
T. Jia, A.-L. Barabási
Control capacity and a random sampling method in exploring controllability of complex networks
Scientific Reports 3:2354, 1-6 (2013)
Read the abstract
Controlling complex systems is a fundamental challenge of network science. Recent advances indicate that control over the system can be achieved through a minimum driver node set (MDS). The existence of multiple MDS's suggests that nodes do not participate in control equally, prompting us to quantify their participations. Here we introduce control capacity quantifying the likelihood that a node is a driver node. To efficiently measure this quantity, we develop a random sampling algorithm. This algorithm not only provides a statistical estimate of the control capacity, but also bridges the gap between multiple microscopic control configurations and macroscopic properties of the network under control. We demonstrate that the possibility of being a driver node decreases with a node's in-degree and is independent of its out-degree. Given the inherent multiplicity of MDS's, our findings offer tools to explore control in various complex systems.
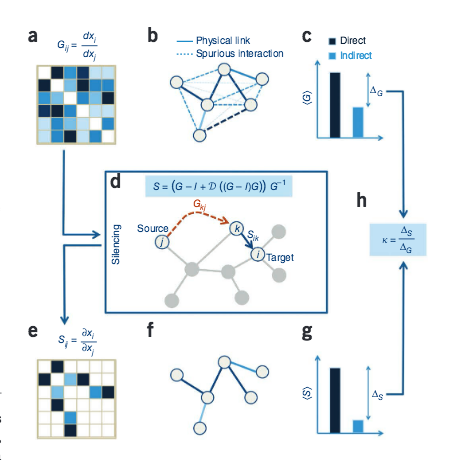
B. Barzel, A.-L. Barabási
Network link prediction by global silencing of indirect correlations
Nature Biotechnology 31: Num 8, 1-8 (2013)
Read the abstract
Predictions of physical and functional links between cellular components are often based on correlations between experimental measurements, such as gene expression. However, correlations are affected by both direct and indirect paths, confounding our ability to identify true pairwise interactions. Here we exploit the fundamental properties of dynamical correlations in networks to develop a method to silence indirect effects. The method receives as input the observed correlations between node pairs and uses a matrix transformation to turn the correlation matrix into a highly discriminative silenced matrix, which enhances only the terms associated with direct causal links. Against empirical data for Escherichia coli regulatory interactions, the method enhanced the discriminative power of the correlations by twofold, yielding >50% predictive improvement over traditional correlation measures and 6% over mutual information. Overall this silencing method will help translate the abundant correlation data into insights about a system's interactions, with applications ranging from link prediction to inferring the dynamical mechanisms governing biological networks.
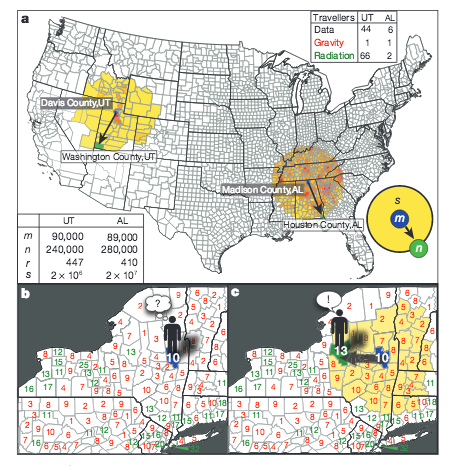
F. Simini, M. González, A. Maritan, A.-L. Barabási
A universal model for mobility and migration patterns
Nature 484, 96-100 (2012)
Read the abstract
Introduced in its contemporary form in 1946, but with roots that go back to the eighteenth century, the gravity law is the prevailing framework with which to predict population movement, cargo shipping volume and inter-city phone calls, as well as bilateral trade flows between nations. Despite its widespread use, it relies on adjustable parameters that vary from region to region and suffers from known analytic inconsistencies. Here we introduce a stochastic process capturing local mobility decisions that helps us analytically derive commuting and mobility fluxes that require as input only information on the population distribution. The resulting radiation model predicts mobility patterns in good agreement with mobility and transport patterns observed in a wide range of phenomena, from long-term migration patterns to communication volume between different regions. Given its parameter-free nature, the model can be applied in areas where we lack previous mobility measurements, significantly improving the predictive accuracy of most of the phenomena affected by mobility and transport processes.
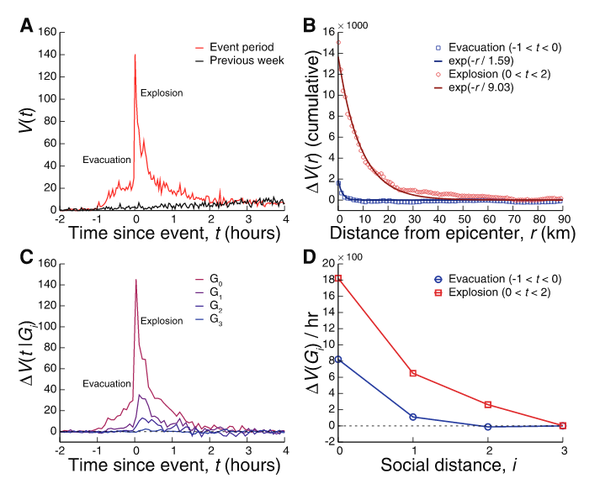
J. P. Bagrow, D. Wang, A.-L. Barabasi
Collective response of human populations to large-scale emergencies
PLoS One 6:3, 1-8 (2011)
Read the abstract
Despite recent advances in uncovering the quantitative features of stationary human activity patterns, many applications,from pandemic prediction to emergency response, require an understanding of how these patterns change when thepopulation encounters unfamiliar conditions. To explore societal response to external perturbations we identified real-timechanges in communication and mobility patterns in the vicinity of eight emergencies, such as bomb attacks andearthquakes, comparing these with eight non-emergencies, like concerts and sporting events. We find that communicationspikes accompanying emergencies are both spatially and temporally localized, but information about emergencies spreadsglobally, resulting in communication avalanches that engage in a significant manner the social network of eyewitnesses.These results offer a quantitative view of behavioral changes in human activity under extreme conditions, with potentiallong-term impact on emergency detection and response.
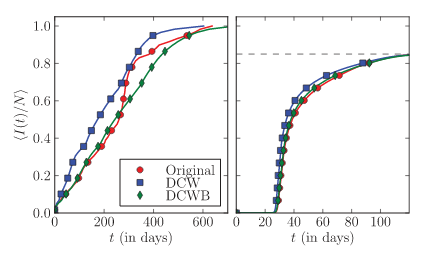
M. Karsai, M. Kivelä, R. K. Pan, K. Kaski, J. Kertész, A.-L. Barabási, J. Saramäki
Small but slow world: How network topology and burstiness slow down spreading
Physical Review E 83, 1-4 (2011)
Read the abstract
While communication networks show the small-world property of short paths, the spreading dynamics in them turns out slow. Here, the time evolution of information propagation is followed through communication networks by using empirical data on contact sequences and the susceptible-infected model. Introducing null models where event sequences are appropriately shuffled, we are able to distinguish between the contributions of different impeding effects. The slowing down of spreading is found to be caused mainly by weight-topology correlations and the bursty activity patterns of individuals.
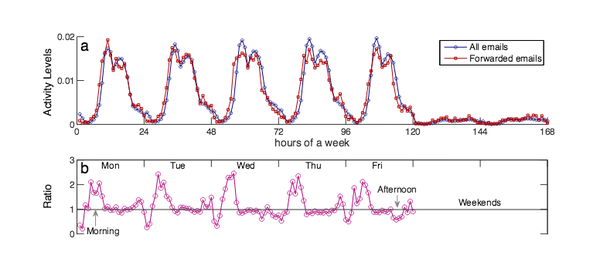
D. Wang, Z. Wen, H. Tong, C.-Y. Lin, C. Song, A.-L. Barabási
Information Spreading in Context
Proceeding for the 20th International World Wide Web Conference, 2011 , 1-10 (2011)
Read the abstract
Information spreading processes are central to human interactions. Despite recent studies in online domains, little is known about factors that could affect the dissemination of a single piece of information. In this paper, we address this challenge by combining two related but distinct datasets, collected from a large scale privacy-preserving distributed social sensor system. We find that the social and organizational context significantly impacts to whom and how fast people forward information. Yet the structures within spreading processes can be well captured by a simple stochastic branching model, indicating surprising independence of context. Our results build the foundation of future predictive models of information flow and provide significant insights towards design of communication platforms.
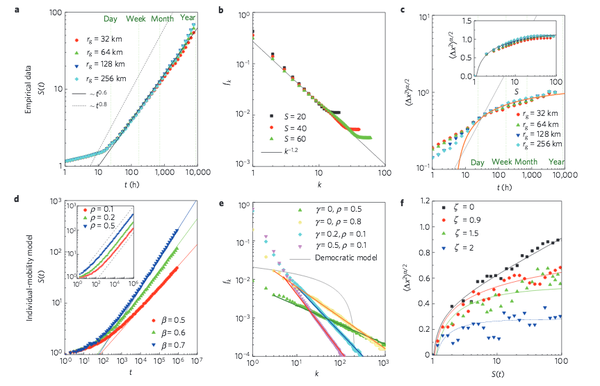
C. Song, T. Koren, P. Wang, A.-L. Barabási
Modelling the scaling properties of human mobility
Nature Physics 7, 713- (2010)
Read the abstract
Individual human trajectories are characterized by fat-tailed distributions of jump sizes and waiting times, suggesting the relevance of continuous-time random-walk (CTRW) models for human mobility. However, human traces are barely random. Given the importance of human mobility, from epidemic modelling to traffic prediction and urban planning, we need quantitative models that can account for the statistical characteristics of individual human trajectories. Here we use empirical data on human mobility, captured by mobile-phone traces, to show that the predictions of the CTRW models are in systematic conflict with the empirical results. We introduce two principles that govern human trajectories, allowing us to build a statistically self-consistent microscopic model for individual human mobility. The model accounts for the empirically observed scaling laws, but also allows us to analytically predict most of the pertinent scaling exponents.
C. Song, Z. Qu, N. Blumm, A.-L. Barabási
Limits of Predictability in Human Mobility
Science 327, 1018-1021 (2010)
Read the abstract
A range of applications, from predicting the spread of human and electronic viruses to city planning and resource management in mobile communications, depend on our ability to foresee the whereabouts and mobility of individuals, raising a fundamental question: To what degree is human behavior predictable? Here we explore the limits of predictability in human dynamics by studying the mobility patterns of anonymized mobile phone users. By measuring the entropy of each individual’s trajectory, we find a 93% potential predictability in user mobility across the whole user base. Despite the significant differences in the travel patterns, we find a remarkable lack of variability in predictability, which is largely independent of the distance users cover on a regular basis.
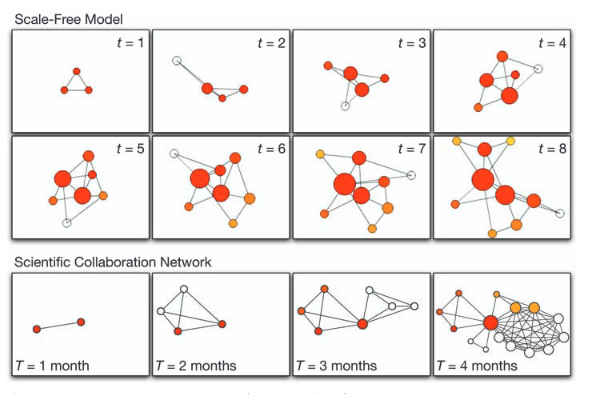
A.-L. Barabási
Scale-Free Networks: A Decade and Beyond
Science 325, 412-413 (2009)
Read the abstract
For decades, we tacitly assumed that the components of such complex systems as the cell, the society, or the Internet are randomly wired together. In the past decade, an avalanche of research has shown that many real networks, independent of their age, function, and scope, converge to similar architectures, a universality that allowed researchers from different disciplines to embrace network theory as a common paradigm. The decade-old discovery of scale-free networks was one of those events that had helped catalyze the emergence of network science, a new research field with its distinct set of challenges and accomplishments.
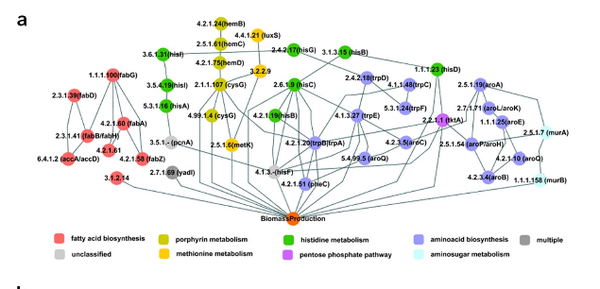
D.-S. Lee, H. Burd, J. Liu, E. Almass, O. Weist, A.-L. Barabási, Z. N. Oltvai, V. Kapatra
Comparative Genome-Scale Metabolic Reconstruction and Flux Balance Analysis of Multiple Staphylococcus aureus Genomes Identify Novel Antimicrobial Drug Targets
Journal of Bacteriology 191:12, 4015–4024 (2009)
Read the abstract
Mortality due to multidrug-resistant Staphylococcus aureus infection is predicted to surpass that of human immunodeficiency virus/AIDS in the United States. Despite the various treatment options for S. aureus infections, it remains a major hospital- and community-acquired opportunistic pathogen. With the emergence of multidrug-resistant S. aureus strains, there is an urgent need for the discovery of new antimicrobial drug targets in the organism. To this end, we reconstructed the metabolic networks of multidrug-resistant S. aureus strains using genome annotation, functional-pathway analysis, and comparative genomic approaches, followed by flux balance analysis-based in silico single and double gene deletion experiments. We identified 70 single enzymes and 54 pairs of enzymes whose corresponding metabolic reactions are predicted to be unconditionally essential for growth. Of these, 44 single enzymes and 10 enzyme pairs proved to be common to all 13 S. aureus strains, including many that had not been previously identified as being essential for growth by gene deletion experiments in S. aureus. We thus conclude that metabolic reconstruction and in silico analyses of multiple strains of the same bacterial species provide a novel approach for potential antibiotic target identification.
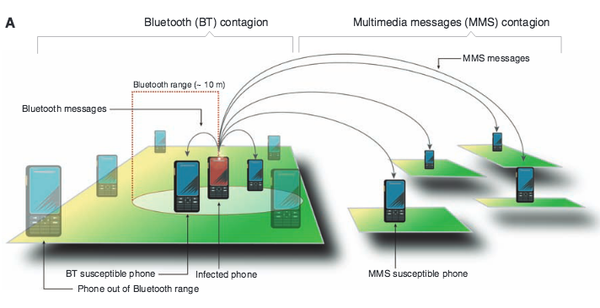
P. Wang, M. Gonzalez, C. A. Hidalgo, A.-L. Barabási
Understanding the spreading patterns of mobile phone viruses
Science 324, 1071-1076 (2009)
Read the abstract
We modeled the mobility of mobile phone users in order to study the fundamental spreading patterns that characterize a mobile virus outbreak. We find that although Bluetooth viruses can reach all susceptible handsets with time, they spread slowly because of human mobility, offering ample opportunities to deploy antiviral software. In contrast, viruses using multimedia messaging services could infect all users in hours, but currently a phase transition on the underlying call graph limits them to only a small fraction of the susceptible users. These results explain the lack of a major mobile virus breakout so far and predict that once a mobile operating system’s market share reaches the phase transition point, viruses will pose a serious threat to mobile communications.
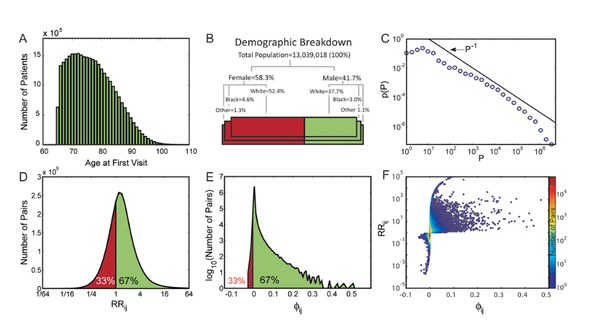
C. A. Hidalgo, N. Blumm, A.-L. Barabási, N. A. Christakis
A dynamic network approach for the study of human phenotypes
PLoS Computational Biology 5:4, 1-11 (2009)
Read the abstract
The use of networks to integrate different genetic, proteomic, and metabolic datasets has been proposed as a viable path toward elucidating the origins of specific diseases. Here we introduce a new phenotypic database summarizing correlations obtained from the disease history of more than 30 million patients in a Phenotypic Disease Network (PDN). We present evidence that the structure of the PDN is relevant to the understanding of illness progression by showing that (1) patients develop diseases close in the network to those they already have; (2) the progression of disease along the links of the network is different for patients of different genders and ethnicities; (3) patients diagnosed with diseases which are more highly connected in the PDN tend to die sooner than those affected by less connected diseases; and (4) diseases that tend to be preceded by others in the PDN tend to be more connected than diseases that precede other illnesses, and are associated with higher degrees of mortality. Our findings show that disease progression can be represented and studied using network methods, offering the potential to enhance our understanding of the origin and evolution of human diseases. The dataset introduced here, released concurrently with this publication, represents the largest relational phenotypic resource publicly available to the research community.
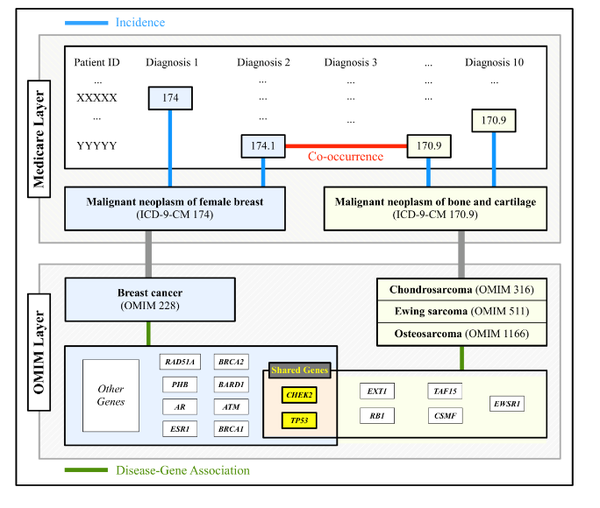
J. Park, D. S. Lee, N. A. Christakis, A.-L. Barabási
The impact of cellular networks on disease comorbidity
Molecular Systems Biology 5:262, 1-7 (2009)
Read the abstract
The impact of disease-causing defects is often not limited to the products of a mutated gene but, thanks to interactions between the molecular components, may also affect other cellular functions, resulting in potential comorbidity effects. By combining information on cellular interactions, disease--gene associations, and population-level disease patterns extracted from Medicare data, we find statistically significant correlations between the underlying structure of cellular networks and disease comorbidity patterns in the human population. Our results indicate that such a combination of population-level data and cellular network information could help build novel hypotheses about disease mechanisms.
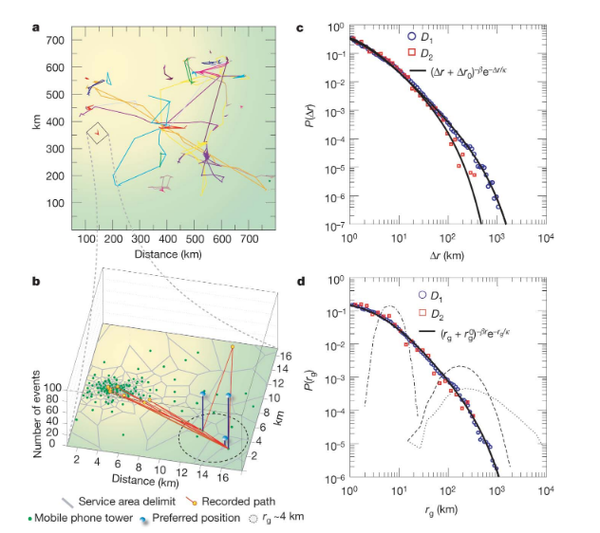
M. C. González, C. A. Hidalgo, A.-L. Barabási
Understanding individual human mobility patterns
Nature 453, 779-782 (2008)
Read the abstract
Despite their importance for urban planning, traffic forecasting and the spread of biological and mobile viruses, our understanding of the basic laws governing human motion remains limited owing to the lack of tools to monitor the time-resolved location of individuals. Here we study the trajectory of 100,000 anonymized mobile phone users whose position is tracked for a six-month period. We find that, in contrast with the random trajectories predicted by the prevailing Levy flight and random walk models, human trajectories show a high degree of temporal and spatial regularity, each individual being characterized by a time independent characteristic travel distance and a significant probability to return to a few highly frequented locations. After correcting for differences in travel distances and the inherent anisotropy of each trajectory, the individual travel patterns collapse into a single spatial probability distribution, indicating that, despite the diversity of their travel history, humans follow simple reproducible patterns. This inherent similarity in travel patterns could impact all phenomena driven by human mobility, from epidemic prevention to emergency response, urban planning and agent-based modeling.
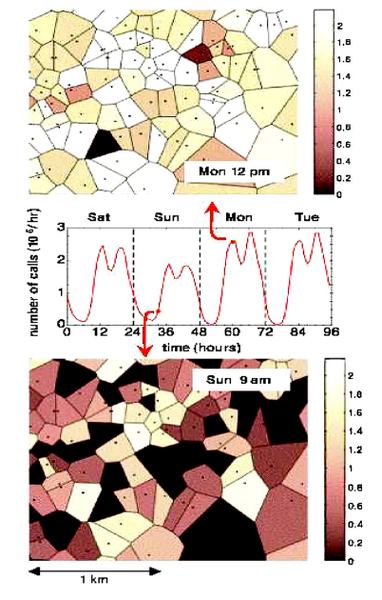
J. Candia, M. C. Gonzalez, P. Wang, T. Schoenharl, G. Madey, A.-L. Barabási
Uncovering individual and collective human dynamics from mobile phone records
Journal of Physics A: Mathematical and Theoretical 41, 1-11 (2008)
Read the abstract
Novel aspects of human dynamics and social interactions are investigated by means of mobile phone data. Using extensive phone records resolved in both time and space, we study the mean collective behavior at large scales and focus on the occurrence of anomalous events. We discuss how these spatiotemporal anomalies can be described using standard percolation theory tools. We also investigate patterns of calling activity at the individual level and show that the interevent time of consecutive calls is heavy-tailed. This finding, which has implications for dynamics of spreading phenomena in social networks, agrees with results previously reported on other human activities.
S. Wuchty, A.-L. Barabási, M.T. Ferdig
Stable evolutionary signal in a Yeast protein interaction network
BMC Evolutionary Biology 60, 8 (2006)
Read the abstract
Background: The recently emerged protein interaction network paradigm can provide novel and important insights into the innerworkings of a cell. Yet, the heavy burden of both false positive and false negative protein-protein interaction data casts doubt on the broader usefulness of these interaction sets. Approaches focusing on one-protein-at-a-time have been powerfully employed to demonstrate the high degree of conservation of proteins participating in numerous interactions; here, we expand his 'node' focused paradigm to investigate the relative persistence of 'link' based evolutionary signals in a protein interaction network of S. cerevisiae and point out the value of this relatively untapped source of information. Results: The trend for highly connected proteins to be preferably conserved in evolution is stable, even in the context of tremendous noise in the underlying protein interactions as well as in the assignment of orthology among five higher eukaryotes. We find that local clustering around interactions correlates with preferred evolutionary conservation of the participating proteins; furthermore the correlation between high local clustering and evolutionary conservation is accompanied by a stable elevated degree of coexpression of the interacting proteins. We use this conserved interaction data, combined with P. falciparum /Yeast orthologs, as proof-of-principle that high-order network topology can be used comparatively to deduce local network structure in nonmodel organisms. Conclusion: High local clustering is a criterion for the reliability of an interaction and coincides with preferred evolutionary conservation and significant coexpression. These strong and stable correlations indicate that evolutionary units go beyond a single protein to include the interactions among them. In particular, the stability of these signals in the face of extreme noise suggests that empirical protein interaction data can be integrated with orthologous clustering around these protein interactions to reliably infer local network structures in non-model organisms.
A.-L. Barabási
Taming complexity
Nature Physics 1, 68-70 (2005)
Read the abstract
The science of networks is experiencing a boom. But despite the necessary multidisciplinary approach to tackle the theory of complexity, scientists remain largely compartmentalized in their separate disciplines. Can they find a common voice?
P.J. Macdonald, E. Almaas, A.-L. Barabási
Minimum spanning trees of weighted scale-free networks
Europhysics Letters 72, 308-314 (2005)
Read the abstract
A complete characterization of real networks requires us to understand the consequences of the uneven interaction strengths between a system’s components. Here we use minimum spanning trees (MSTs) to explore the effect of correlations between link weights and network topology on scale-free networks. Solely by changing the nature of the correlations between weights and network topology, the structure of the MSTs can change from scale-free to exponential. Additionally, for some choices of weight correlations, the efficiency of the MSTs increases with increasing network size, a result with potential implications for the design and scalability of communication networks.
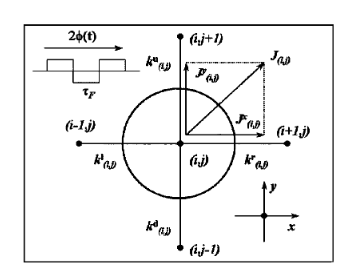
M. A. Makeev, I. Derenyi, A.-L. Barabási
Emergence of large-scale vorticity during diffusion in a random potential under an alternating bias
Physical Review E 71, 026112 (2005)
Read the abstract
Conventional wisdom indicates that the presence of an alternating driving force will not change the longterm behavior of a Brownian particle moving in a random potential. Although this is true in one dimension, here we offer direct evidence that the inevitable local symmetry breaking present in a two-dimensional random potential leads to the emergence of a local ratchet effect that generates large-scale vorticity patterns consisting of steady-state net diffusive currents. For small fields the spatial correlation function of the current follows a logarithmic distance dependence, while for large external fields both the vorticity and the correlations gradually disappear. We uncover the scaling laws characterizing this unique pattern formation process, and discuss their potential relevance to real systems.
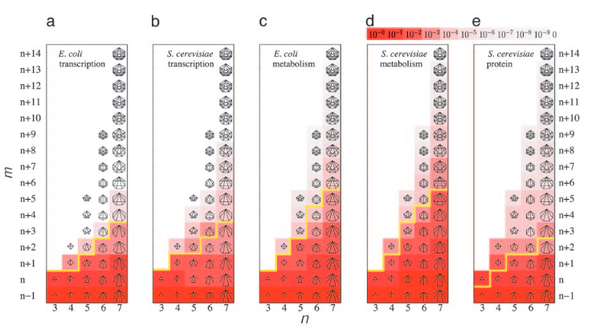
A. Vazquez, J. G. Oliveira, A.-L. Barabási
Inhomogeneous evolution of subgraphs and cycles in complex networks
Physical Review E 71, 025103 (2005)
Read the abstract
Subgraphs and cycles are often used to characterize the local properties of complex networks. Here we show that the subgraph structure of real networks is highly time dependent: as the network grows, the density of some subgraphs remains unchanged, while the density of others increase at a rate that is determined by the network’s degree distribution and clustering properties. This inhomogeneous evolution process, supported by direct measurements on several real networks, leads to systematic shifts in the overall subgraph spectrum and to an inevitable overrepresentation of some subgraphs and cycles.
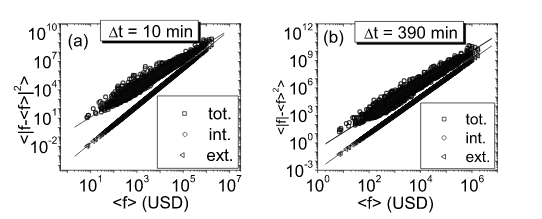
Z. Eisler, J. Kertesz, S.-H. Yook, A.-L. Barabási
Multiscaling and non-universality in fluctuations of driven complex systems
Europhysics Letters 69, 664-670 (2005)
Read the abstract
For many externally driven complex systems neither the noisy driving force, nor the internal dynamics are a priori known. Here we focus on systems for which the timedependent activity of a large number of components can be monitored, allowing us to separate each signal into a component attributed to the external driving force and one to the internal dynamics. We propose a formalism to capture the potential multiscaling in the fluctuations and apply it to the high-frequency trading records of the New York Stock Exchange. We find that on the time scale of minutes the dynamics is governed by internal processes, while on a daily or longer scale the external factors dominate. This transition from internal to external dynamics induces systematic changes in the scaling exponents, offering direct evidence of non-universality in the system.
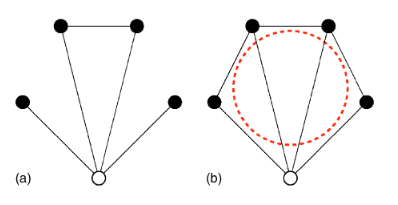
A. Vazquez, R. Dobrin, D. Sergi, J.-P. Eckmann, Z. N. Oltvai, A.-L. Barabási
The topological relationship between the large-scale attributes and local interactions patterns of complex networks
Proceedings of the National Academy of Sciences 101, 17940-17945 (2004)
Read the abstract
Recent evidence indicates that the abundance of recurring elementary interaction patterns in complex networks, often called subgraphs or motifs, carry significant information about their function and overall organization. Yet, the underlying reasons for the variable quantity of different subgraph types, their propensity to form clusters, and their relationship with the networks’ global organization remain poorly understood. Here we show that a network’s large-scale topological organization and its local subgraph structure mutually define and predict each other, as confirmed by direct measurements in five well studied cellular networks. We also demonstrate the inherent existence of two distinct classes of subgraphs, and show that, in contrast to the low-density type II subgraphs, the highly abundant type I subgraphs cannot exist in isolation but must naturally aggregate into subgraph clusters. The identified topological framework may have important implications for our understanding of the origin and function of subgraphs in all complex networks.
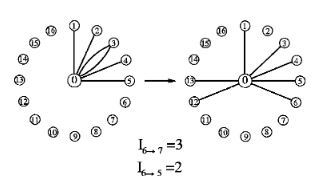
G. Palla, I. Farkas, I. Derenyi, A.-L. Barabási, T. Vicsek
Reverse engineering of linking preferences from network restructuring
Physical Review E 70, 046115 (2004)
Read the abstract
We provide a method to deduce the preferences governing the restructuring dynamics of a network from the observed rewiring of the edges. Our approach is applicable for systems in which the preferences can be formulated in terms of a single-vertex energy function with fskd being the contribution of a node of degree k to the total energy, and the dynamics obeys the detailed balance. The method is first tested by Monte Carlo simulations of restructuring graphs with known energies; then it is used to study variations of real network systems ranging from the coauthorship network of scientific publications to the asset graphs of the New York Stock Exchange. The empirical energies obtained from the restructuring can be described by a universal function fskd,−k ln k, which is consistent with and justifies the validity of the preferential attachment rule proposed for growing networks.
A.-L. Barabási, R. Albert
Emergence of scaling in random networks
Science 286, 509–512 (1999)
Read the abstract
Systems as diverse as genetic networks or the World Wide Web are best described as networks with complex topology. A common property of many large networks is that the vertex connectivities follow a scale-free power-law distribution. This feature was found to be a consequence of two generic mechanisms: (i) networks expand continuously by the addition of new vertices, and (ii) new vertices attach preferentially to sites that are already well connected. A model based on these two ingredients reproduces the observed stationary scale-free distributions, which indicates that the development of large networks is governed by robust self-organizing phenomena that go beyond the particulars of the individual systems.
M. A. de Menezes, A.-L. Barabási
Fluctuations in network dynamics
Physical Review Letters 92, 28701 (2004)
Read the abstract
Most complex networks serve as conduits for various dynamical processes, ranging from mass transfer by chemical reactions in the cell to packet transfer on the Internet.We collected data on the time dependent activity of five natural and technological networks, finding that for each the coupling of the flux fluctuations with the total flux on individual nodes obeys a unique scaling law. We show that the observed scaling can explain the competition between the system’s internal collective dynamics and changes in the external environment, allowing us to predict the relevant scaling exponents.
I. Farkas, I. Derenyi, H. Jeong, Z. Neda, Z. N. Oltvai, E. Ravasz, A. Schubert, A.-L. Barabási, T. Vicsek
Networks in life: scaling properties and eigenvalue spectra
Physica A 314, 25-34 (2002)
Read the abstract
We analyze growing networks ranging from collaboration graphs of scientists to the network ofsimilarities de9ned among the various transcriptional pro9les ofliving cells. For the explicit demonstration ofthe scale-free nature and hierarchical organization ofthese graphs, a deterministic construction is also used. We demonstrate the use ofdetermining the eigenvalue spectra of sparse random graph models for the categorization of small measured networks.
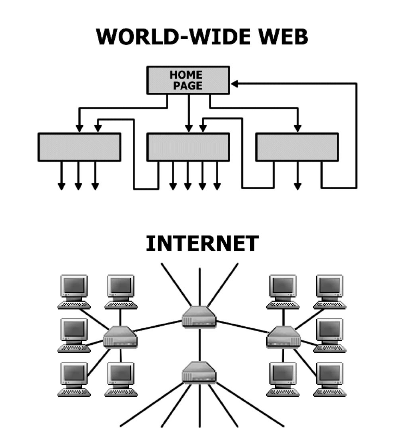
R. Albert, A.-L. Barabási
Statistical mechanics of complex networks
Reviews of Modern Physics 74, 47-97 (2002)
Read the abstract
Complex networks describe a wide range of systems in nature and society. Frequently cited examples include the cell, a network of chemicals linked by chemical reactions, and the Internet, a network of routers and computers connected by physical links. While traditionally these systems have been modeled as random graphs, it is increasingly recognized that the topology and evolution of real networks are governed by robust organizing principles. This article reviews the recent advances in the field of complex networks, focusing on the statistical mechanics of network topology and dynamics. After reviewing the empirical data that motivated the recent interest in networks, the authors discuss the main models and analytical tools, covering random graphs, small-world and scale-free networks, the emerging theory of evolving networks, and the interplay between topology and the network’s robustness against failures and attacks.
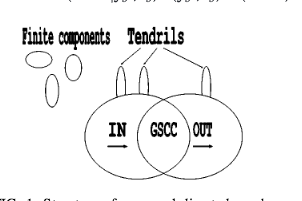
N. Schwartz, R. Cohen, D. ben-Avraham, A.-L. Barabási, S. Havlin
Percolation in directed scale-free networks
Physical Review E 66, 015104 (2002)
Read the abstract
Many complex networks in nature have directed links, a property that affects the network’s navigability and large-scale topology. Here we study the percolation properties of such directed scale-free networks with correlated in and out degree distributions. We derive a phase diagram that indicates the existence of three regimes, determined by the values of the degree exponents. In the first regime we regain the known directed percolation mean field exponents. In contrast, the second and third regimes are characterized by anomalous exponents, which we calculate analytically. In the third regime the network is resilient to random dilution, i.e., the percolation threshold is pe-->1.
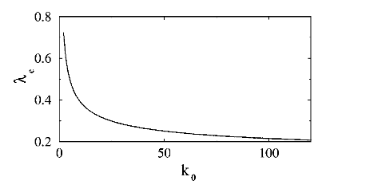
Z. Dezso, A.-L. Barabási
Halting viruses in scale-free networks
Physical Review E 65, 055103 (2002)
Read the abstract
The vanishing epidemic threshold for viruses spreading on scale-free networks indicate that traditional methods, aiming to decrease a virus’ spreading rate cannot succeed in eradicating an epidemic. We demonstrate that policies that discriminate between the nodes, curing mostly the highly connected nodes, can restore a finite epidemic threshold and potentially eradicate a virus. We find that the more biased a policy is towards the hubs, the more chance it has to bring the epidemic threshold above the virus’ spreading rate. Furthermore, such biased policies are more cost effective, requiring less cures to eradicate the virus.
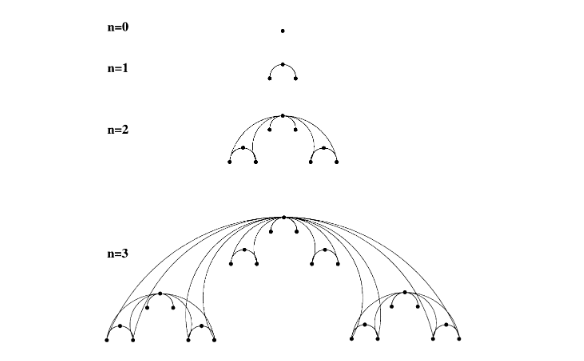
A.-L. Barabási, E. Ravasz, T. Vicsek
Deterministic scale-free networks
Physica A 299, 559–564 (2001)
Read the abstract
Scale-free networks are abundant in nature and society, describing such diverse systems as the world wide web, the web of human sexual contacts, or the chemical network of a cell. All models used to generate a scale-free topology are stochastic, that is they create networks in which the nodes appear to be randomly connected to each other. Here we propose a simple model that generates scale-free networks in a deterministic fashion. We solve exactly the model, showing that the tail of the degree distribution follows a power law.
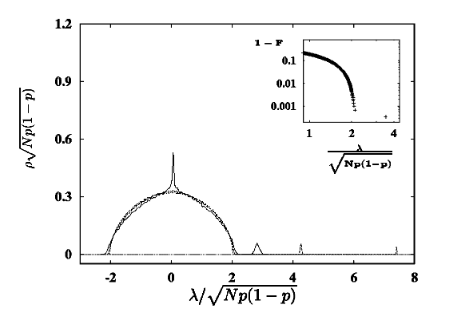
I. J. Farkas, I. Derenyi, A.-L. Barabási, T. Vicsek
Spectra of “real-world” graphs: beyond the semicircle law
Physical Review E Physical Review, 026704 (2001)
Read the abstract
Many natural and social systems develop complex networks that are usually modeled as random graphs. The eigenvalue spectrum of these graphs provides information about their structural properties. While the semicircle law is known to describe the spectral densities of uncorrelated random graphs, much less is known about the spectra of real-world graphs, describing such complex systems as the Internet, metabolic pathways, networks of power stations, scientific collaborations, or movie actors, which are inherently correlated and usually very sparse. An important limitation in addressing the spectra of these systems is that the numerical determination of the spectra for systems with more than a few thousand nodes is prohibitively time and memory consuming. Making use of recent advances in algorithms for spectral characterization, here we develop methods to determine the eigenvalues of networks comparable in size to real systems, obtaining several surprising results on the spectra of adjacency matrices corresponding to models of real-world graphs. We find that when the number of links grows as the number of nodes, the spectral density of uncorrelated random matrices does not converge to the semicircle law. Furthermore, the spectra of real-world graphs have specific features, depending on the details of the corresponding models. In particular, scale-free graphs develop a trianglelike spectral density with a power-law tail, while small-world graphs have a complex spectral density consisting of several sharp peaks. These and further results indicate that the spectra of correlated graphs represent a practical tool for graph classification and can provide useful insight into the relevant structural properties of real networks.
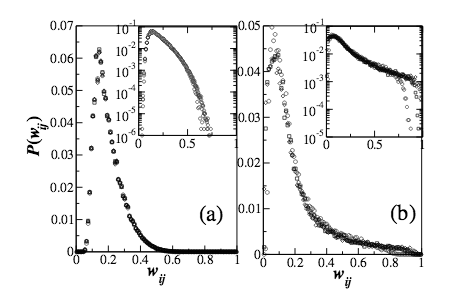
S. H. Yook, H. Jeong, A.-L. Barabási, Y. Tu
Weighted evolving networks
Physical Review Letters 86, 5835-5838 (2001)
Read the abstract
Many biological, ecological, and economic systems are best described by weighted networks, as the nodes interact with each other with varying strength. However, most evolving network models studied so far are binary, the link strength being either 0 or 1. In this paper we introduce and investigate the scaling properties of a class of models which assign weights to the links as the network evolves. The combined numerical and analytical approach indicates that asymptotically the total weight distribution converges to the scaling behavior of the connectivity distribution, but this convergence is hampered by strong logarithmic corrections.
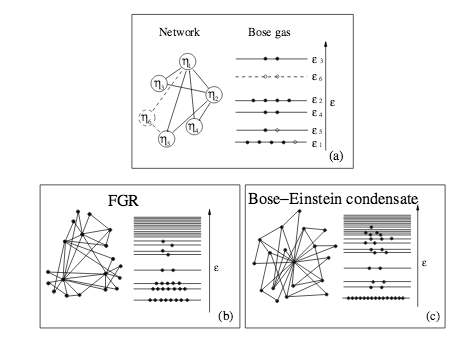
G. Bianconi, A.-L. Barabási
Bose-Einstein condensation in complex networks
Physical Review Letters 86, 5632–5635 (2001)
Read the abstract
The evolution of many complex systems, including the World Wide Web, business, and citation networks, is encoded in the dynamic web describing the interactions between the system’s constituents. Despite their irreversible and nonequilibrium nature these networks follow Bose statistics and can undergo Bose-Einstein condensation. Addressing the dynamical properties of these nonequilibrium systems within the framework of equilibrium quantum gases predicts that the “first-mover-advantage,” “fit-get-rich,” and “winner-takes-all” phenomena observed in competitive systems are thermodynamically distinct phases of the underlying evolving networks.
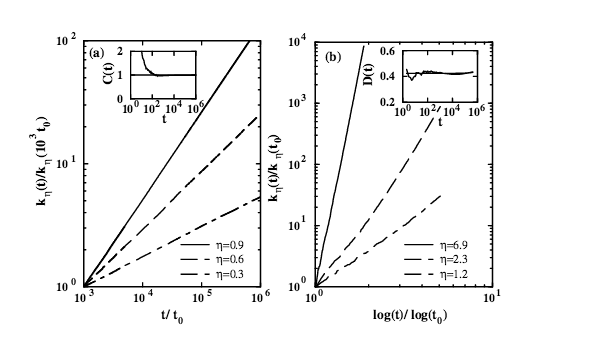
G. Bianconi, A.-L. Barabási
Competition and multiscaling in evolving networks
Europhysics Letters 54, 436-442 (2001)
Read the abstract
The rate at which nodes in a network increase their connectivity depends on their fitness to compete for links. For example, in social networks some individuals acquire more social links than others, or on the www some webpages attract considerably more links than others. We find that this competition for links translates into multiscaling, i.e. a fitnessdependent dynamic exponent, allowing fitter nodes to overcome the more connected but less fit ones. Uncovering this fitter-gets-richer phenomenon can help us understand in quantitative terms the evolution of many competitive systems in nature and society.
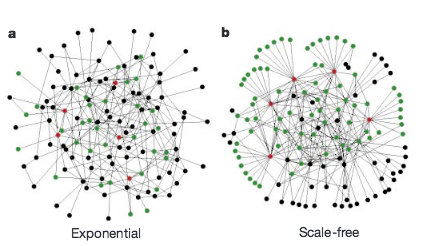
R. Albert, H. Jeong, A.-L. Barabási
Error and attack tolerance of complex networks
Nature 406, 378–482 (2000)
Read the abstract
Here we demonstrate that error tolerance is not shared by all redundant systems: it is displayed only by a class of inhomogeneouslywired networks,called scale-free networks, which include theWorld-WideWeb, the Internet, social networks and cells. We find that such networks display an unexpected degree of robustness, the ability of their nodes to communicate being unaffected even by unrealistically high failure rates.However, error tolerance comes at a high price in that these networks are extremely vulnerable to attacks (that is, to the selection and removal of a few nodes that play a vital role in maintaining the network’s connectivity). Such error tolerance and attack vulnerability are generic properties of communication networks.
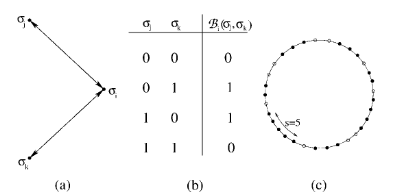
R. Albert, A.-L. Barabási
Dynamics of complex systems: scaling laws for the period of boolean networks
Physical Review Letters 84, 5660-5663 (2000)
Read the abstract
Boolean networks serve as models for complex systems, such as social or genetic networks, where each vertex, based on inputs received from selected vertices, makes its own decision about its state. Despite their simplicity, little is known about the dynamical properties of these systems. Here we propose a method to calculate the period of a finite Boolean system, by identifying the mechanisms determining its value. The proposed method can be applied to systems of arbitrary topology, and can serve as a roadmap for understanding the dynamics of large interacting systems in general.
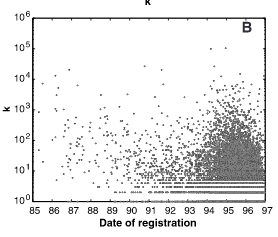
A.-L. Barabási, R. Albert, H. Jeong, G. Bianconi
Power-law distribution of the world wide web
Science 287, 2115 (2000)
Read the abstract
Barabasi and Albert propose an improved version of the Erdos-Renyi theory of random networks to account for the scaling properties of a number of systems, including the link structure of the World Wide Web (WWW). The theory they present, however, is inconsistent with empirically observed properties of the Web link structure.
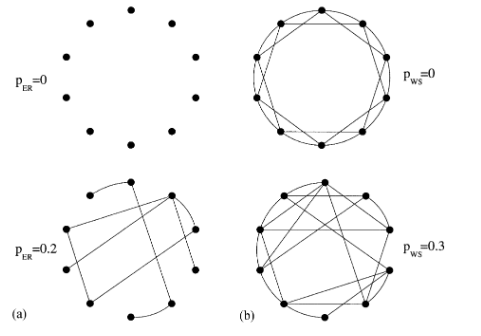
A.-L. Barabási, R. Albert, H. Jeong
Mean-field theory for scale-free random networks
Physica A 272, 173–187 (1999)
Read the abstract
Random networks with complex topology are common in Nature, describing systems as diverse as the world wide web or social and business networks. Recently, it has been demonstrated that most large networks for which topological information is available display scale-free features. Here we study the scaling properties of the recently introduced scale-free model, that can account for the observed power-law distribution of the connectivities. We develop a mean-feld method to predict the growth dynamics of the individual vertices, and use this to calculate analytically the connectivity distribution and the scaling exponents. The mean-feld method can be used to address the properties of two variants of the scale-free model, that do not display power-law scaling.
R. Albert, A.-L. Barabási
Topology of evolving networks: local events and universality
Physical Review Letters 85, 5234-5237 (2000)
Read the abstract
Networks grow and evolve by local events, such as the addition of new nodes and links, or rewiring of links from one node to another. We show that depending on the frequency of these processes two topologically different networks can emerge, the connectivity distribution following either a generalized power law or an exponential. We propose a continuum theory that predicts these two regimes as well as the scaling function and the exponents, in good agreement with numerical results. Finally, we use the obtained predictions to fit the connectivity distribution of the network describing the professional links between movie actors.